Hugh Bird

Redistributing vortex particles

July 25, 2019

An inevitable problem with regularised vortex particle methods is the spreading of vortex particles. Shear layers are stretched, and the particles that constitute the shear layers are spread out. The particles, since they no longer overlap, now fail to represent the vorticity field.

This can be demonstrated using an unsteady aerofoil case. Using LiftingLineTheory.jl’s LAUTAT (large amplitude unsteady thin aerofoil) implementation:

julia> 	using LiftingLineTheory

julia> 	eldredge_max = eldredge_ramp(4, 1, 3, 5, 7,11, 1, 1)
	43.9999999994421

julia> 	kinematics = RigidKinematics2D(x->0, x->deg2rad(30)*eldredge_ramp(x, 1,3,5,7,11,1,1)/eldredge_max, -0.5);

julia> 	prob = LAUTAT(;kinematics=kinematics, dt=0.015);

julia> 	nsteps = Int(ceil(10/0.015))
	667

julia> 	for i = 1 : nsteps
		advance_one_step(prob)
	end
	   
julia> 	to_vtk(prob, "basiscase")

This produces:

Basis case

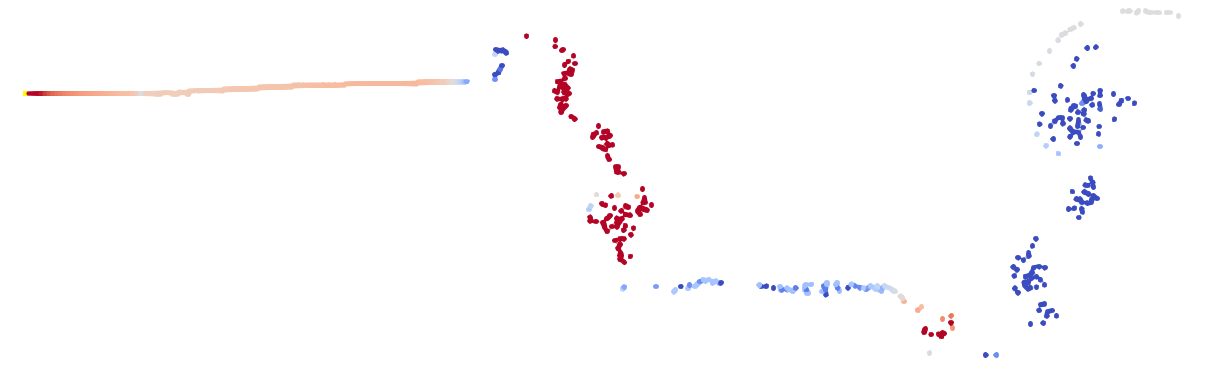
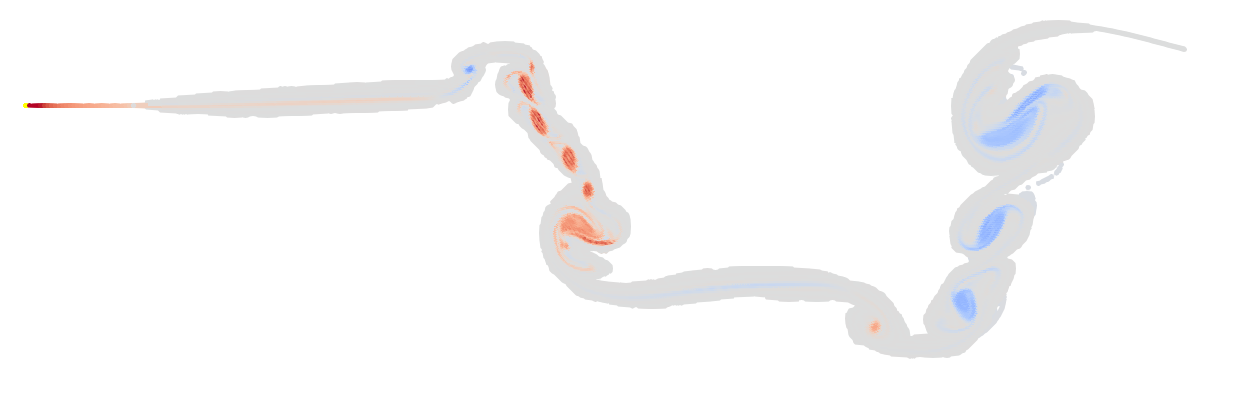
The vortex particles are visualised with size matching their regularisation distance. In areas of the wake near vortices, the particles don’t overlap. This is bad.

An attempt to fix this is to use more vortex particles, using the same regularisation distance:

julia> 	prob = LAUTAT(;kinematics=kinematics, dt=0.0015, reg_dist=0.025);

julia> 	nsteps = Int(ceil(10/0.0015))
	6667

julia> 	for i = 1 : nsteps
		advance_one_step(prob)
	end

Small dt, same regularisation

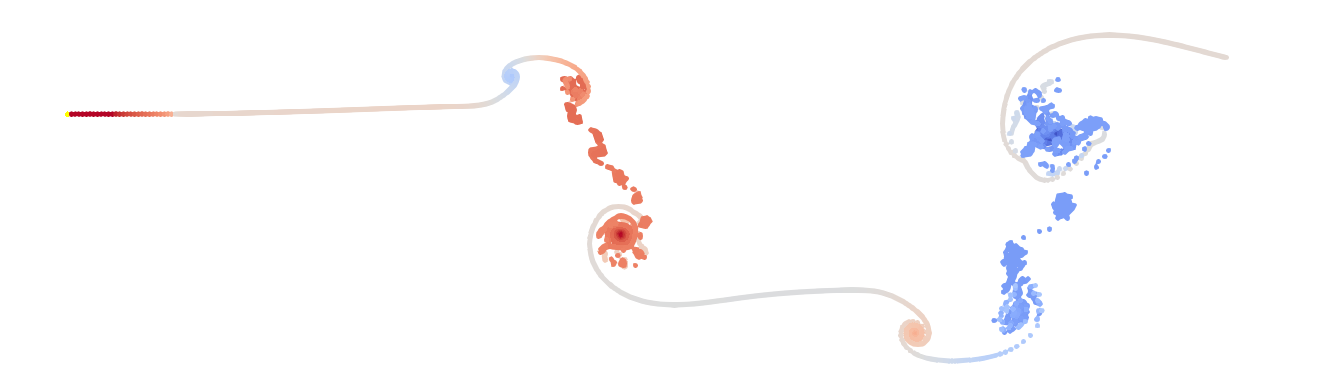
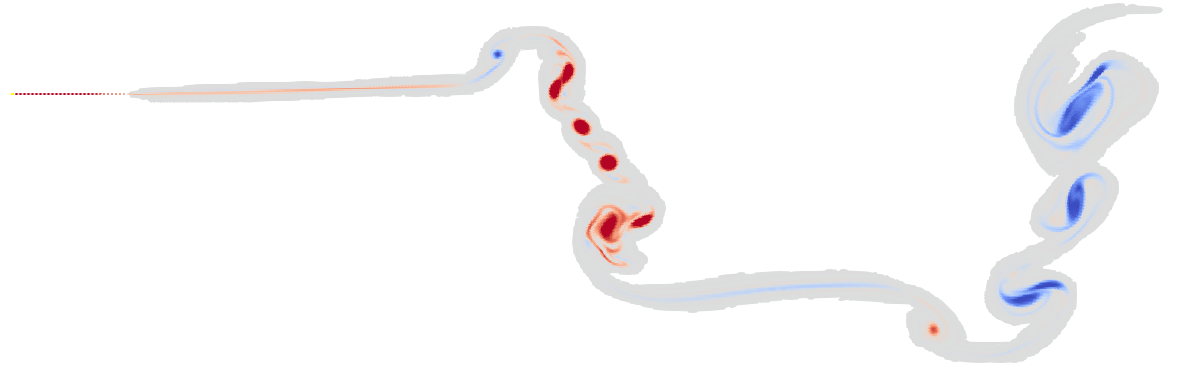
Ah, not fixed. Lets try even smaller:

julia> 	prob = LAUTAT(;kinematics=kinematics, dt=0.00015, reg_dist=0.025);

julia> 	nsteps = Int(ceil(10/0.00015))
	66667

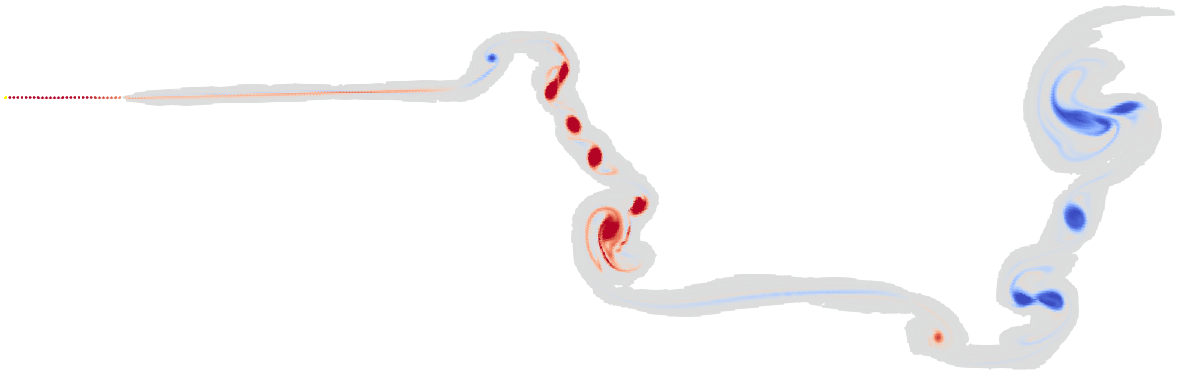
This is arguably excessively small, resulting in quite a few timesteps with quite a few particles. Two episodes of Yes Minister later, we obtain a solution:

Really small dt, same regularisation

And… nope, we still don’t have the well resolved solution we’re looking for. Just producing more particles is not the solution. We need a way to compensate for the spreading of our vortex particles.

The usual solution to this is redistributing particles onto a lattice. The old particles are replaced with new ones which represent the same vorticity field, but whilst alleviating our problem.

The new lattice has spacing \(h\), which is also used to obtain normalised distances \(U\) and \(W\) of a gridpoint from vortex particles in the \(x\) and \(y\) directions. A redistribution function \(\Lambda(U, W) = \Lambda(U) \Lambda(W)\) is then used to obtain the strength vortex placed on a new grid-point. The vorticity \(\alpha\) associated with a grid-point at \(\mathbf{x}\) is then given by

\[\alpha = \sum_i \alpha_i \Lambda \left(\frac{|(\mathbf{x} - \mathbf{x}_i)_x | }{h}, \frac{|(\mathbf{x} - \mathbf{x}_i)_ z| } { h } \right)\]

where \(\alpha_i\) and \(\mathbf{x}_i\) are the vortices and locations of the \(i\)th particle in the original vorticity field.

This most simple redistribution method is to lump vorticity to the nearest grid-point:

\[\Lambda_0(U) = \begin{cases} 1 & \text{ if } U < \frac{1}{2}\\ 0 & \text{ otherwise} \end{cases}\]

We can apply this to our unsteady thin aerofoil problem. Remeshing on every step would be excessive, so we might want to redistribute every 10 steps or so. This makes our solver semi-Lagrangain. Adding this to the LAUTAT code:

julia> 	using CVortex

julia> 	prob = LAUTAT(;kinematics=kinematics, dt=0.015);

julia> 	nsteps = Int(ceil(10/0.015))
	667

julia> 	for i = 1 : nsteps
		advance_one_step(prob)
		if i%10 == 0
			ppos = prob.te_particles.positions[1:end-1, :]
			pvort = prob.te_particles.vorts[1:end-1]
			ppos, pvort, ~ = CVortex.redistribute_particles_on_grid(ppos, pvort, lambda0_redistribution(), 0.015)
			prob.te_particles.positions = vcat(ppos, prob.te_particles.positions[end,:]')
			prob.te_particles.vorts = vcat(pvort, prob.te_particles.vorts[end])
		end
	end

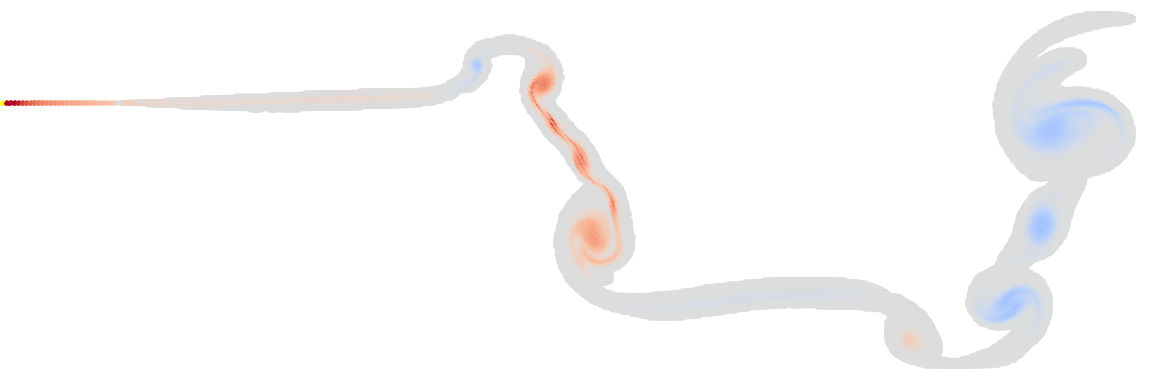
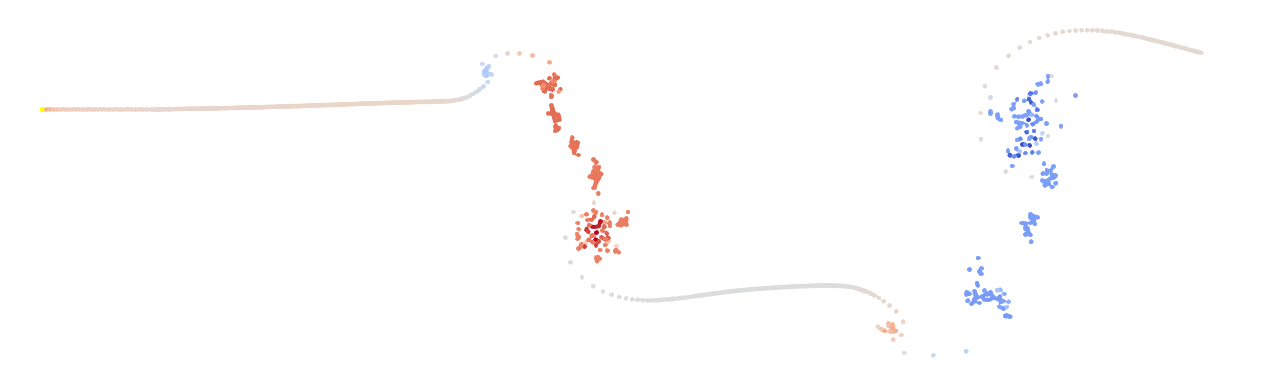
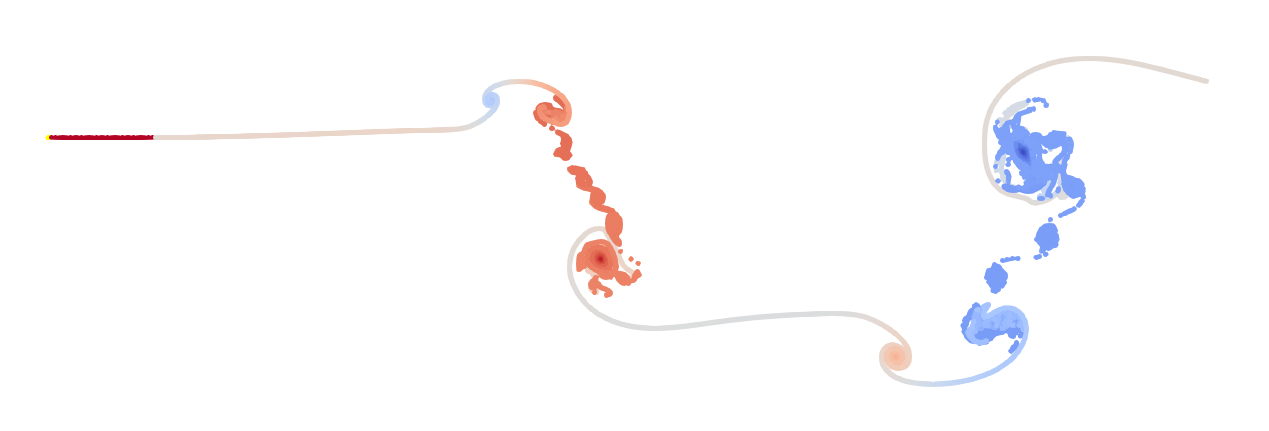
This scheme gives rather disappointing results:

Lambda0 regridded case

The scheme is discontinuous, which leads to numerical noise. On the plus side, it results in fewer vortices than the original implementation.

High order, non-discontinuous schemes are desirable.

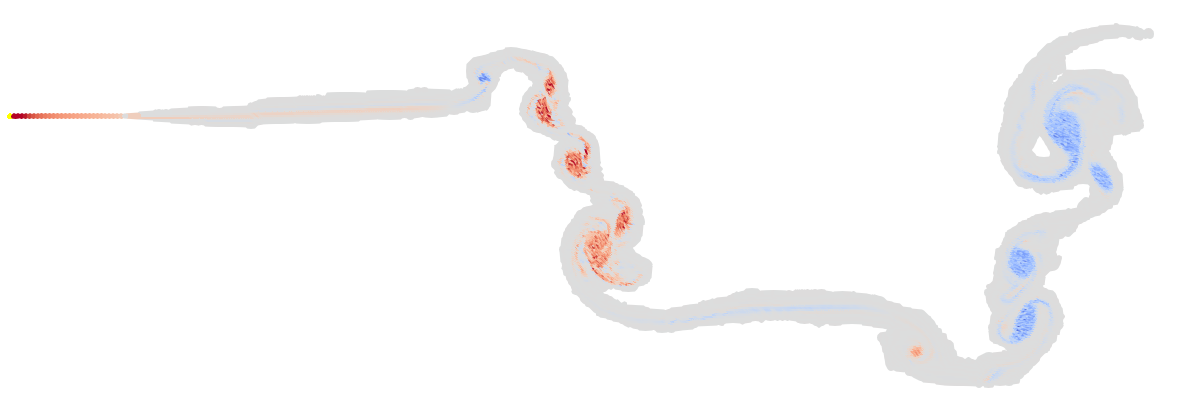
\[\Lambda_1(U) = \begin{cases} 1-U & \text{ if } U \leq 1\\ 0 & \text{ otherwise} \end{cases}\]

Such as scheme removes the discontinuity and gives far better looking results. However it is also dissipative. Consequently, the solution of this scheme is a little closer to what one might expect from CFD. Lambda1 regridded case

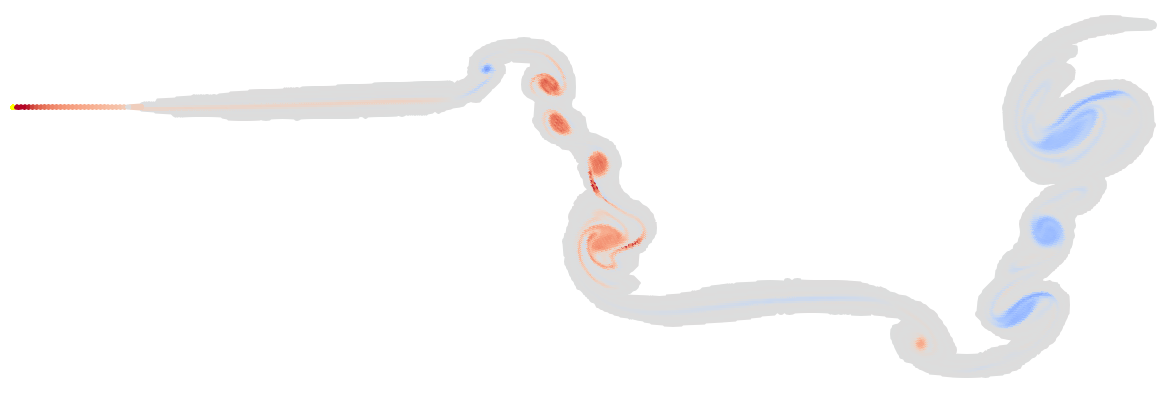
A higher order scheme still is the \(\Lambda_2\) scheme. This is once again discontinuous.

\[\Lambda_2(U) = \begin{cases} 1-U^2 & \text{ if } 0 \leq U < \frac{1}{2}\\ \frac{1}{2}(1-U)(2-U) & \text{ if } \frac{1}{2} \leq U < \frac{3}{2}\\0 & \text{ otherwise} \end{cases}\]

These discontinuities make the solution look sparkly. Lambda2 regridded case

Finally we reach the higher order schemes. Both the \(\Lambda_3\) and \(M_4'\) are - according to Winckelmans - most often used. They are as follows:

\[\Lambda_3(U) = \begin{cases} \frac{1}{2}(1-U^2)(2-U) & \text{ if } 0 \leq U < 1\\ \frac{1}{6}(1-U)(2-U)(3-U) & \text{ if } 1 \leq U \leq 2\\0 & \text{ otherwise} \end{cases}\] \[M_4'(U) = \begin{cases} 1 - \frac{5}{2}U^2+\frac{3}{2}U^3 & \text{ if } 0 \leq U \leq 1\\ \frac{1}{2}(1-U)(2-U)^2 & \text{ if } 1 \leq U \leq 2\\0 & \text{ otherwise} \end{cases}\]

The \(\Lambda_3\) gives:

Lambda3 regridded case

And the \(M_4'\) scheme gives:

M4' regridded case

So we have two slightly different solutions. Is either better?

We can use more refined solutions for comparison. Setting \(dt=h=0.015/2=0.0075\) and the grid spacing we obtain solution redistributed with the \(\Lambda_4\) and \(M_4'\) scheme respectively:

Lambda3 regridded case

M4' regridded case

So what am I taking from these refined cases? The most distinctive difference in the unrefined case between the two schemes is the large blue vortex in the middle on the right of the image. For the unrefined \(\Lambda_3\) scheme it is circular, whilst for the unrefined \(M_4'\) case it has two trailing legs. For the refined cases, it becomes circular for the \(M_4'\) case and legged for the \(\Lambda_3\) case. Not useful. However, for many of the other vortices, the \(\Lambda_3\) scheme is more consistent between refinement levels. Overall, without further examination of the repercussions of different ODE solvers and solver settings, I suspect that comparing the redistribution functions is a futile exercise.

Finally, a few notes.

Recommended reading:

Hugh Bird

A Post-graduate research student at the University of Glasgow, United Kingdom.

  • About